Motion P1788/M007.01_NaI: NO, several NaIs please
I vote no to Motion 7 but I do also fall into the camp of "please give me
several standardized NaIs please."
From my perspective, there are two main problems with trying to define away
all invalid operations by returning empty:
-- empty does not "propagate universally," since it can be absorbed in
union operations; and
-- any assertion about empty set is always vacuously true; for certain
practical interval algorithms this can give misleading results.
Here is an example (it is not in domain of computer graphics, so has been
approved by the Sunfish police for me to share).
Suppose the user gives us the function
g(x) := cos(x0)+sin(x1/exp(x0))+sqr(x0/x1)
and the function
f(x) := ln(g(x)).
Then a user asks us to perform a branch-and-bound method, to within some
tolerance, over the domain X = ( [-4,0], [1,5] ) in order to find a subset
S := { x in X | f(x) <= 0, x is real, f(x) is real }.
So there should be no vacuous truth: if f(x) is undefined (not real) at some
x, then all those x should not be members of S.
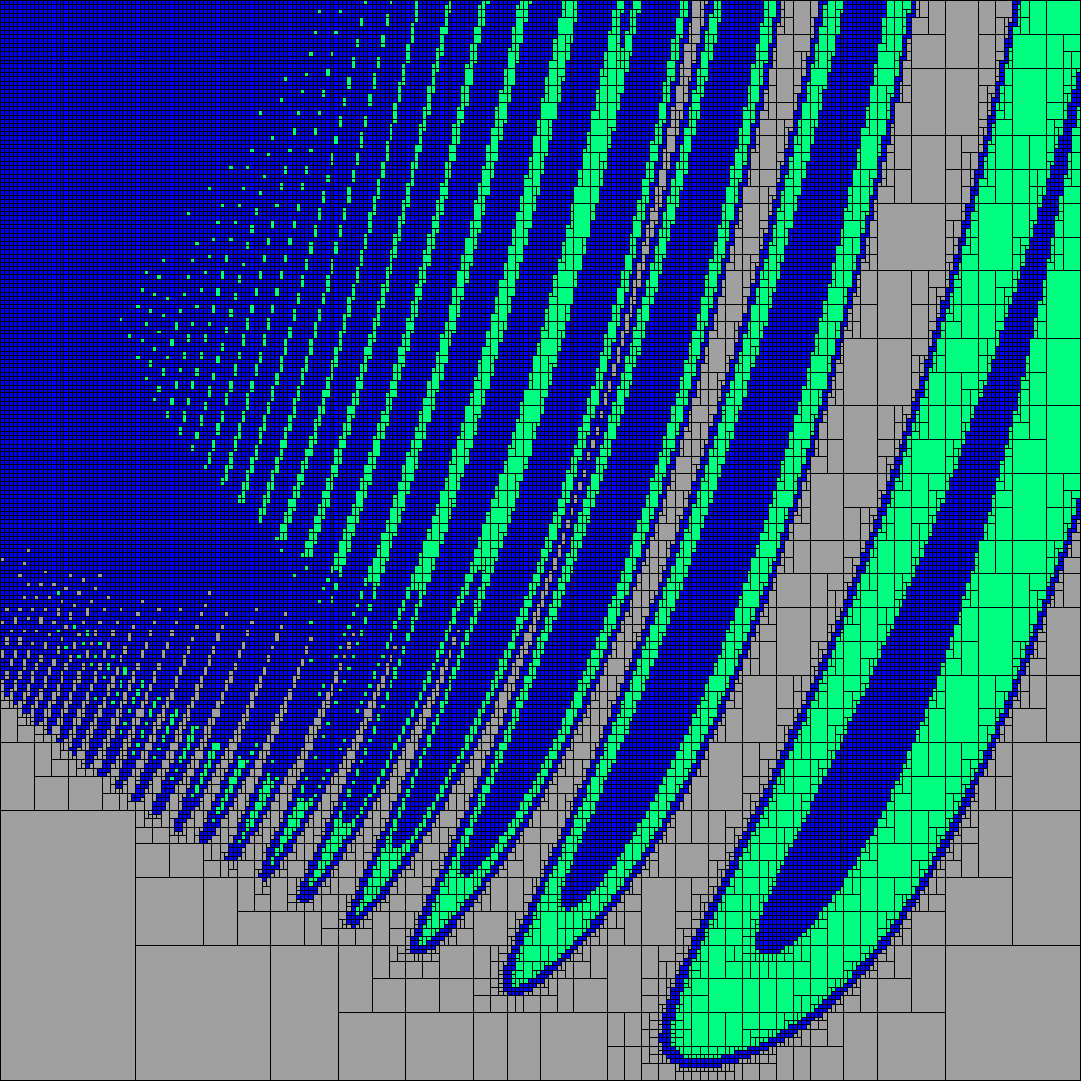
We define the branch-and-bound method as
if isEmpty(f(X')) then delete X' // yellow
else if f(X') > 0 then delete X' // gray
else if f(X') <= 0 then accept X' // green
else if eps(X') then mark X' indeterminate // blue
else bisect X'
where X' is any sub-box of X and eps(X') is a function to determine if the
sub-box meets tolerance criteria or not.
Assume for the moment that g(X') always returns the optimal range enclosure
in exact arithmetic. If g(X') = [-1,0.3] for some X', then ln([-1,0.3]) is a
domain overflow, so (according to some current proposals) the interval
argument [-1,0.3] is intersected with the natural domain (0,Inf) of the
logarithm function
ln([-1,0.3]&(0,Inf)) = ln((0,0.3]) = (-Inf,ln(0.3)].
However, consider the consequences carefully, i.e.,
(-Inf,ln(0.3)] <= 0
is a true statement. So X' is accepted as a false (misleading) solution.
Paving A shows the actual results.
If we change our assumption that domain overflows are instead treated as
invalid operations and generate NaI, then things are different. In this
case, if g(X') = [-1,0.3] for some X', then ln([-1,0.3]) is an invalid
operation, i.e.,
ln([-1,0.3]) = NaI.
This leads to the condition
NaI <= 0,
which is false. So X' is not accepted as a solution, and instead X' is
further subdivided. Paving B shows the results.
Imagine that the user tells us, for any real x, if f(x) > 0 or f(x) is not
real, then something really, really bad will happen. For example, the rocket
will blow-up on the launching pad. So it is imperative that no such x is
admitted into the solution set.
In Paving B, the green boxes are a conservative approximation of this
solution set. If there are some x in the blue boxes that the user is
concerned about, they can adjust the tolerance criteria and keep subdividing
the blue boxes to any desired resolution until they find their answer. But
the solution set of green boxes will always be conservative, in order to
prevent the pending disaster that may otherwise occur.
NaI with payload may also be of further aid in this example, since it could
allow the branch-and-bound algorithm to avoid unnecessary bisections of the
blue boxes in certain portions of the paving.
Nate Hayes
Sunfish Studio, LLC