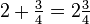More on Vincent's comments on text
Vincent, P1788
More on Vincent's comments:
On 31 Jan 2013, at 17:13, Vincent Lefevre wrote:
> §8.8.4, paragraph 2: the relation between this paragraph for y_ill
> with nonempty y and §8.8.3 is not clear.
If we move to the "pragmatic" definition of ill, I hope this is no longer a problem.
> §8.8.7: With the rule given on NaI, code ending with something like
> (e.g. for piecewise functions):
> y = convexHull(u_du,v_dv)
> dy = dx
> or
> y_dy = convexHullDec(u_du,v_dv)
> may be wrong if NaI can occur in intermediate results! There should
> be a note with some warning. I suspect problems may occur in practice
> with parameterized intervals (a function may become nowhere defined
> for some values of the parameter). This is a problem with specific
> rules for NaI: here a NaI can be produced by evaluating a function
> that is never defined, but having such an operation on intervals is
> not necessarily a user error.
I sort of see what you mean but would like a specific example. Would this, which might happen in CAD, give an example?
Write an interval extension of f(t), defined to be the closest distance of the point (t,0) on the x-axis, to the disk
D: x^2 + (y-b)^2 <= r^2,
where b>=0, r>0 are given parameters. Then for r>b there is an interval round t=0 in which f(t)=0; for r=b this shrinks to the single point [0,0]; for r<b there is no such interval.
> §8.8.9, Example (i): Replace "2½" by "2+½"? I don't know whether "2½"
> is a common notation. However it may be ambiguous.
It's the usual British notation. E.g. Wikipedia:
> Mixed numbers
> A mixed numeral (often called a mixed number, also called a mixed fraction) is the sum of a non-zero integer and a proper fraction. This sum is implied without the use of any visible operator such as "+". For example, in referring to two entire cakes and three quarters of another cake, the whole and fractional parts of the number are written next to each other: 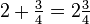
> .
> §8.8.10, definition of "com": about "and the computed interval f(x)
> is bounded", I would add (perhaps in the notes, at least more clearly
> than in the third note) that this condition is needed only at Level 2
> (since all the intervals we consider in the standard are closed), and
> an unbounded interval is necessarily a consequence of an overflow.
In view of the discussions between Guillaume, me and you about this, these notes need rewriting to make the key facts clearer. I'm attempting this on the lines you suggest.
> §8.8.10, "Each arithmetic operation gives com as its local decoration
> if the conditions (30) are satisfied.", just after (31): is this a
> "shall" or a "should"? And I would add "in" or "of" before "(30)",
> since (30) seems to be the whole table rather than the conditions.
shall. And yes. Both done.
> §8.8.10, "The propagation rule [...] is" (next line): replace "rule
> [...] is" by "rules [...] are" (the plural is used in the notes and
> it looks better to me)?
Done
> §8.8.11: Since decorations trv, emp, ill and dac are mentioned,
> I suppose that compressed arithmetic is specified only for the
> set-based flavor (and the common one). This should be said.
It's part of the set-based chapter. Need more be said?
John